M1 - Cinématique du point
Résumé
Il s'agira ici d'étudier le mouvement d'un point matériel sans s'intéresser aux causes qui lui ont donner naissance. Nous nous intéresserons donc aux notions de référentiel et de système de coordonnées cartésiennes, cylindriques et sphériques. Dans chaque cas, nous préciserons les vecteurs importants pour la description du mouvement: position, déplacement élémentaire, vitesse et accélération.Capacité exigibles
- Dessiner les surfaces sur lesquelles l'une des coordonnées est uniforme dans les différents systèmes de coordonnées.
- Savoir calculer l'équation d'une trajectoire.
- Calculer l'expression des vecteurs position, vitesse et accélération ainsi que leur norme en coordonnées cartésiennes et cylindriques.
- Exprimer les vecteurs de la base cylindrique en fonction des vecteurs de la base cartésienne.
- En coordonnées cartésiennes, savoir calculer l'équation d'une trajectoire à partir des équations horaires du mouvement.
- Reconnaitre un mouvement rectiligne, rectiligne uniforme, circulaire uniforme en coordonnées cartésiennes et cylindriques.
- Dans le cas d'un mouvement circulaire, relier la valeur de la vitesse du point à celle de la vitesse angulaire.
Polycopié de cours
QCM d'entrainement
Sujet de TD
Pour aller plus loin
Systèmes de coordonnées
Memento sur les différents systèmes de coordonnées
Cours vidéo détaillé d'E-learning Physique sur les coordonnées polaires
Cours vidéo de Physics Girl (anglophone) sur les bases de la cinématique
M2 - Dynamique du point
Résumé
Après avoir étudié comment décrire un mouvement au chapitre précédent, nous nous intéressons à ce qui le cause ou le modifie. Pour se faire, nous introduisons le concept de force et passons en revue quelques forces très utilisées en mécanique. Le lien entre force et changement de mouvement est assuré par les trois lois de Newton, détaillées dans ce chapitre. Du point de vue mathématique, l'application de la deuxième de ces lois (le PFD) sera l'occasion de se familiariser avec les équations différentielles et leur résolution.Capacité exigibles
- Citer les trois lois de Newton et leurs conséquences immédiates.
- Connaitre des exemples de référentiels galiléens usuels.
- Identifier le système étudié, le référentiel galiléen et le repère adapté au problème.
- Connaitre les expressions mathématiques des forces usuelles : poids, frottements fluides, poussée d'Archimède.
- Établir un bilan des forces et les représenter sur un schéma.
- Appliquer le PFD, en déduire l'équation du mouvement et la résoudre.
- Savoir reconnaitre une équation différentielle du premier ordre et la résoudre.
Polycopié de cours
QCM d'entrainement
Sujet de TD
Pour aller plus loin
Dynamique
Vidéo d'e-penser sur les débuts de la mécanique moderne
Article de David Louapre (Science étonnante) sur la relativité de Galilée
Enigme de Physics Girl (anglophone) sur la poussée d'Archimède
Vidéo de la BBC (anglophone) montrant la chute d'une boule de bowling et d'une plume dans le vide
M3 - Signaux sinusoïdaux et oscillateur harmonique
Résumé
Après un bref rappel sur les fonctions trigonométriques, nous allons utiliser les outils vus aux chapitres précédents pour les appliquer aux mouvements périodiques et en particulier, aux mouvements sinusoïdaux. Ceci nous permettra d'introduire un modèle très général que nous raffinerons dans les chapitres suivants: celui de l'oscillateur harmonique.Capacité exigibles
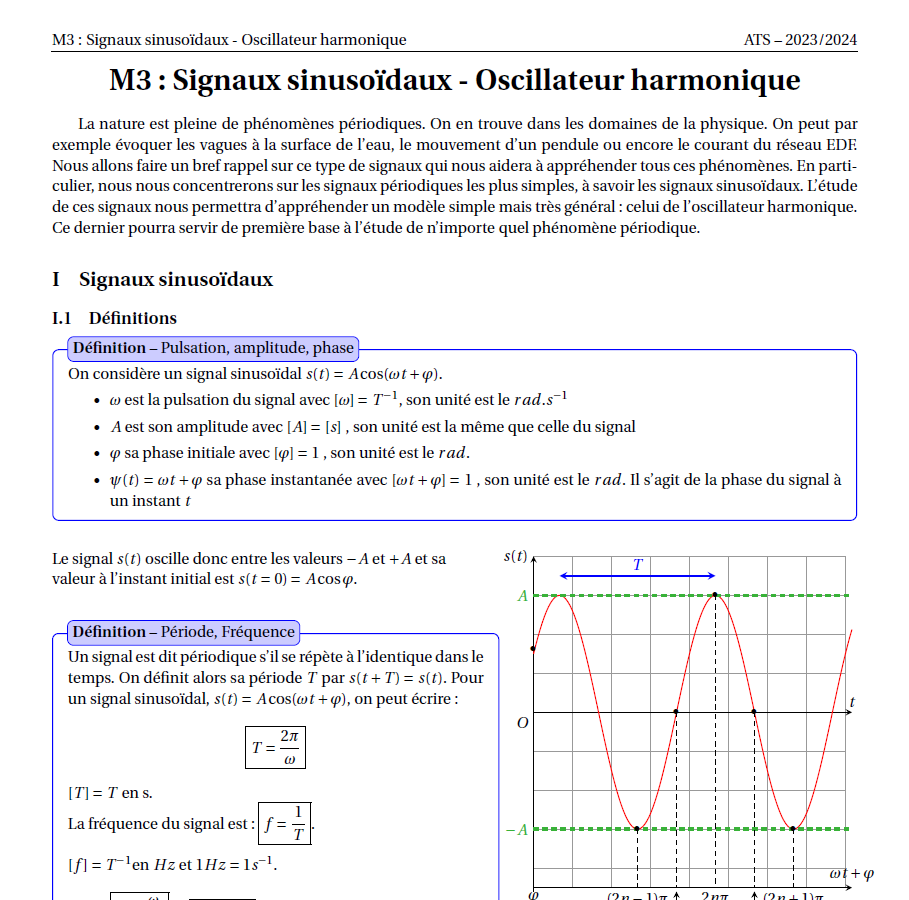
- Identifier l'amplitude, la phase, la pulsation, la période et la fréquence d'un signal sinusoïdal.
- Calculer ou mesurer le déphasage entre deux signaux sinusoïdaux.
- Etudier graphiquement des signaux sinusoïdaux.
- Connaître l'expression générale de la force de rappel élastique et l'adapter à une situation décrite dans un énoncé.
- Reconnaitre et résoudre l'équation différentielle de l'oscillateur harmonique.
Polycopié de cours
QCM d'entrainement
Sujet de TD